Benford's Analysis of COVID-19 Data

Introduction

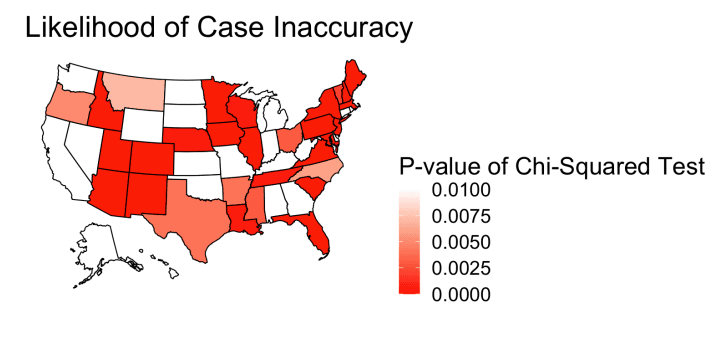
During my time at the Wharton Data Science Academy from May to July 2021, I conducted a research project applying Benford's Law to analyze COVID-19 data. Benford's Law predicts the frequency distribution of leading digits in many real-life datasets, and deviations from this distribution can indicate anomalies or potential data manipulation. This analysis aimed to assess the integrity of reported COVID-19 case numbers.

Solution

Utilizing R and Exploratory Data Analysis (EDA) techniques, I examined over 28,000 COVID-19 case entries. By calculating the logarithm of p-values for case and death data, I modeled a linear regression to plot p-values ranging from 0.1 to 0.05, providing insights into the conformity of the data with Benford's Law.

Data Collection and Preparation

Collected a dataset comprising over 28,000 COVID-19 case entries, ensuring data cleanliness and readiness for analysis by handling missing values and standardizing formats.

Application of Benford's Law

Applied Benford's Law to the dataset to analyze the frequency distribution of leading digits in reported COVID-19 cases and deaths, identifying deviations that could indicate anomalies or inconsistencies.

Statistical Modeling

Calculated the logarithm of p-values for case and death data, modeling a linear regression to plot p-values ranging from 0.1 to 0.05, providing a visual representation of data conformity to Benford's Law.

This research project provided valuable insights into the application of statistical methods for data validation. Key learnings include:

Overall, this experience enhanced my proficiency in statistical analysis and data science methodologies, emphasizing the importance of data integrity in public health reporting.